產品分類
熱門資訊
聯(lián)系我們/Contact Us
地址：上海市奉賢區(qū)青村鎮(zhèn)星火公路188號1幢
陳經理：15021366229 陳經理：18616962314
QQ：76667015
網址:mm595.cn
Email:[email protected]
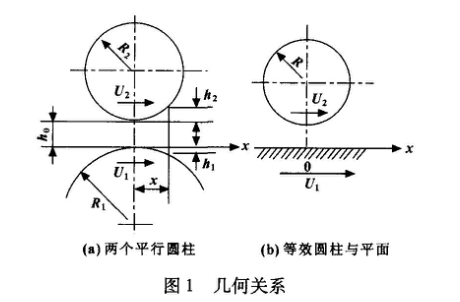
皮帶輸送機托輥的彈流潤滑分析
文章來源：http://mm595.cn 發(fā)布時間：2018-08-09 11:20 瀏覽次數(shù)：
皮帶輸送機已有200多年的歷史,早在1795年美國就用它來輸送谷物。1920年以后,皮帶輸送機成為煤炭、鐵礦石的主要輸送設備,部分取代汽車、船舶及火車運輸,以求節(jié)省運輸費用。近年來,隨著工業(yè)和技術的發(fā)展,作為現(xiàn)代散狀物料連續(xù)運輸?shù)闹饕O備,皮帶輸送機已廣泛應用于冶金、礦山、化工、港口和電站等工業(yè)領域。大運量、長距離、高帶速的散狀物料輸送已成為皮帶輸送機的發(fā)展主流。
皮帶運輸機托輥軸承的潤滑狀況可以簡化為無限長線接觸的彈流潤滑情況來分析,線接觸問題屬于一維彈流潤滑問題。根據(jù)參考資料,將軸承內圈和圓柱滾子等效成一個平面和一個等效的圓柱體,并根據(jù)幾何關系求出了等效圓柱體的半徑。利用 Fortran語盲和 Origin繪圖軟件對皮帶運輸機托輥軸承的潤滑狀況進行數(shù)值模擬與仿真。
幾何關系
根據(jù)推導 Reynolds方程時的基本假設(4),即:與膜厚相比,支撐表面的曲率半徑很大,因此可以忽略由表面曲率引起的速度方向的變化。托輥軸承的潤滑系統(tǒng)可以轉換成由一個平面和一個等效圓柱組成的潤滑系統(tǒng),但轉化時必須保證間隙形狀不變。
圖1中,R1、R2分別代表兩接觸的圓柱體,當研究圓柱滾子軸承的潤滑狀況時,將R2看作是圓柱棍子的半徑,將R1看作是軸承內圈的半徑。根據(jù)機械手冊和各個生產廠家的數(shù)據(jù),選用NU207E型號的軸承,內徑d=35mm,外徑D=72m,B=17mm。因此通過幾何關系可以計算出:R1=22mm,R2=9mm。
因此就可以根據(jù)以上幾何關系計算出等效圓柱體的半徑R
相關新聞
- 皮帶輸送機撕裂故障及其防護措施分析2018-11-15
- 滾筒輸送機的發(fā)展及現(xiàn)狀研究（二）2018-11-15
- 滾筒輸送機的發(fā)展及現(xiàn)狀研究（一）2018-11-15
- 皮帶輸送機固體物料稱重給料系統(tǒng)設計初探2018-11-01
- 摩擦式積放滾筒輸送機裝置的設計2018-11-01
- 滾筒輸送機PLC控制技術在空調生產系統(tǒng)中的應用2018-11-01
